Gradients, animation and more fun with OpenGL

Continuing on the theme of my previous OpenGL post, I wanted to share some notes on more OpenGL experiments I tried my hand at.

In this round I wanted to setup a sort of playground for me to be able to simply create new directories and start writing some code without having to worry about the compiling. I didn't want to just copy over the entire root with the libraries and include folder each time either, so I decided to set up a parent directory which contains all of the shared libraries and each experiment is a sub-directory with its own makefile which takes care of compilation and launching the experiment.

Diving into each of the experiments also caught me off-guard with linear algebra concepts that I hadn't had to think about really since my college days, which at the very least was nostalgic.

Directory Setup

So like I said I wanted to set up the directory structure to be able to quickly create a subdirectory and use some shared libraries in the parent directory. Practically this is what that the root directory looks like:

│   .gitattributes
│   .gitignore
│   glew32.dll
│   glew32.lib
│   glfw3.dll
│   libglfw3.a
│   libglfw3dll.a
│   LICENSE
│   README.md
│
├───Experiments
│   ├───Experiment1
│   │   │   main.cpp
│   │   │   makefile
│   │   │
│   │   └───shaders
│   │           fragment_shader.glsl
│   │           vertex_shader.glsl
│   │
│   └───Experiment2
│       │   main.cpp
│       │   makefile
│       │
│       └───shaders
│               fragment_shader.glsl
│               vertex_shader.glsl
│
└───include
    ├───GL
    ├───GLFW
    └───glm
        ├───CMakeFiles
        ├───detail
        ├───ext
        ├───gtc
        ├───gtx
        └───simd

With this directory structure I can then add the following makefile to each subdirectory to compile and run the code:

build:
	g++ -o a.out main.cpp ../../libglfw3dll.a ../../glew32.dll -I../../include -lglew32 -lglfw3 -lopengl32
	./a.out

This might all be fairly pedestrian to most C++ heads but admittedly took me a while to figure out since C++ isn't my day to day language. 😅 Please feel free to let me know if there is a better way to do this.

OpenGL Mathematics

In the previous post I described using the GLFW and GLEW libraries and why they are being used. In this post I added a third library to the common libraries being used: OpenGL Mathematics or more commonly referred to as GLM. GLM is a mathematics library for graphics software and allows you to add a lot of simple and convenient functionality to GLSL.

Experiment 1 - Pulsating animation

The first thing I wanted to learn about was getting some animation into my drawings. The biggest takeaway from this experiment for me was learning about Uniforms. The Book of Shaders does a great job explaining these but the TLDR; is to think of Uniforms as bridges between the CPU and the GPU, allowing you to send information between two to influence the calculations on the GPU. In this instance, we used a Uniform to send the number of elapsed seconds since the start of the animation and used that with a GLSL sin wave function to move the red channel of the triangle's color vector between its minimum and maximum, resulting in a pulsating effect.

Experiment link.

Experiment 2 - Gradients

Next I want to see some variation within the triangle itself in the form of a gradient. This time we added a new uniform u_resolution which contains the measurements of the window we are rendering our triangle inside. We use this to normalize the coordinate of the fragment, in order to use it as a value in our color vector. The coordinate of the pixel we render is coming from the built in variable gl_FragCoord and is the value we are normalizing with the u_resolution.

Experiment link.

Experiment 3 - Rainbow gradient

Next I wanted to go beyond a simple gradient and draw a triangle with a rainbow gradient. I found a ShaderToy with a 3 color gradient and was able to use it for what I wanted. The mix function allows us to provide two colors and provide the percentage of mixing that we would like to perform on the two colors. We again use the normalized pixel coordinate to determine the mixing percentage. We also use the step function to determine the mix percentage of the start and end colors with a halfway point 0.5 specified for where we want the transition (to and from green) to occur.

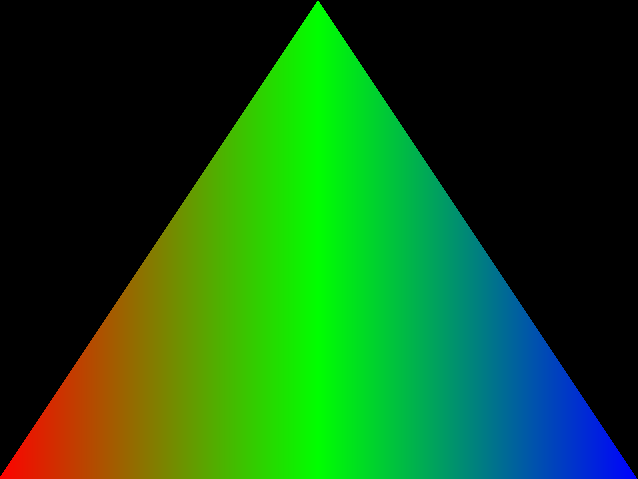
If we use a static 1.0 percentage instead of the step function we see this instead:

And if we use a static 0.0 percentage instead of the step function we see this instead:

Link to experiment.

Experiment 4 - Animation and Matrix Transformation

Next I wanted to learn how to start adding in animation to my drawings. This is where the GLM library I mentioned at the start of the post comes in. Animation can be performed by passing a transformation matrix via a uniform from the C++ code to the vertex shader. In the vertex shader the current pixel position is then multiplied with the transformation matrix to produce the new coordinates. This can be used to scale, rotate or translate coordinates, and using some linear algebra we are able to pass a rotation matrix to the vertex shader, apply it to each coordinate and perform a rotation on our triangle.

As always an in-depth explanation can be found in the Book of Shaders.

Experiment link.

Experiment 5 - Lots of triangles

For the final experiment I wanted to draw lots of these triangles. I wanted to use a technique called instancing that I think I'm going to be using in a future experiment. Instancing is a more efficient way to draw the same model lots of times in a scene versus sending each model draw command separately. You are also able to define different transformations for each instance, and in my case I want to draw the same model (my triangle) lots of times with my transformation being a translation/offset so you can see each triangle distinctly. Here's what that looks like in practice:

Experiment link.